La technique de réfraction utilisée pour la recherche du cylindre correcteur d’une prescription n’a que très peu évolué depuis de nombreuses années. La raison principale en est la limite imposée par les réfracteurs subjectifs à défilement de verres par pas de 0.25 dioptrie. Aujourd’hui, avec les réfracteurs à variations continues de puissances permettant d’agir simultanément, et avec grande précision, sur la sphère, le cylindre et l’axe de la correction, il est possible de développer de nouvelles techniques de réfraction. Cet article décrit les principes d’une nouvelle méthode vectorielle de détermination du cylindre correcteur et présente la logique d’un algorithme automatisé de recherche du cylindre qui lui est associé.
Hélène Starynkevitch - Responsable d’Etudes R&D, Division Instruments - Essilor International
Hélène Starynkevitch est diplômée du BTS Opticien Lunetier de l'Institut et Centre d'Optométrie (ICO) à Bures sur Yvette (2013) et de l'université d'Orsay Paris Sud XI en Ingénierie de la Santé, Spécialité Science de la Vision (2016). Elle est actuellement ingénieur d'étude au sein du département R&D d'Essilor Instruments. Elle travaille au développement de méthodes et algorithmes d'examen de vue associées aux nouveaux instruments et à la conception des interfaces pour les praticiens. Elle est aussi responsable d'études d'optométrie, portant sur la comparaison des instruments et/ou sur les méthodologies d'examen de vue. Hélène a aussi oeuvré comme bénévole pour VisionSoliDev pour la réalisation d'examen de vue pour les personnes défavorisées.
Gildas Marin - Responsable d’Etudes R&D, Service R&D Sciences de la Vision -Essilor International
Gildas Marin a obtenu son diplôme d’ingénieur en optique en 1993 et a poursuivi ses études par une thèse en imagerie médicale à l’institut d’optique et l’hôpital de la Pitié-Salpêtrière (Paris), soutenue en 1997. Depuis 2006, il est responsable d’étude en sciences de la vision chez Essilor International. Ses domaines de recherche principaux sont la modélisation de la vision, la simulation des effets optiques et des performances visuelles, en particulier de l’impact des aberrations optiques sur la vision. Plus récemment, il a travaillé sur l’amélioration des méthodes de réfraction. A partir de 2015, il a été responsable du programme de recherche sur le développement et la validation des algorithmes et des méthodes de réfraction précise implémentées dans le Vision-R™ 800 et l’offre AVA™ (Advanced Vision Accuracy).
Dominique Meslin - Directeur Solutions de Réfraction, Division Instruments -Essilor International
Opticien et Optométriste de formation, Dominique Meslin a effectué la plus grande partie de sa carrière chez Essilor, tout d’abord au sein du département Recherches et Développement puis dans différents postes de Marketing et Communication techniques en France ainsi qu’aux États-Unis. Il a été pendant 10 ans le Directeur d’Essilor Academy Europe puis responsable des Relations Professionnelles pour Essilor Europe. Il est
aujourd’hui en charge des nouvelles Solutions de Réfraction au sein de la Division Instruments d’Essilor International. Tout au long de sa carrière, Dominique Meslin a animé de nombreux séminaires pour les professionnels de la vision. Il est l’auteur de plusieurs publications scientifiques et de nombreuses publications techniques d’Essilor, dont la série des « Cahiers d’Optique Oculaire ».
Depuis près d’un siècle, la technique de réfraction utilisée pour la recherche du cylindre correcteur d’un patient n’a que très peu évolué. Elle consiste, universellement, à utiliser un cylindre croisé dit « de Jackson » et à étudier la variation de ses effets pour différentes positions, afin de rechercher l’axe du cylindre puis sa puissance et, ensuite, à en ajuster l’effet sur la puissance de la sphère. Si cette technique a peu évolué depuis son invention, c’est essentiellement en raison du fait que les réfracteurs subjectifs ont eux mêmes peu évolué : depuis près d’un siècle, ils permettent uniquement de présenter des verres sphériques et cylindriques devant les yeux d’un patient, par pas de puissance de 0.25 dioptrie et pas d’axe de 5 degrés, et sans qu’il ne soit possible d’agir simultanément sur la sphère, le cylindre et l’axe de la correction.
Aujourd’hui, grâce aux nouveaux réfracteurs à variations continues de puissances, contrôlés avec une résolution de 0.01 dioptrie sur la puissance et de 0.1 degré sur l’axe, et qui permettent d’agir simultanément sur la sphère, le cylindre et son axe(*), il est possible de proposer une nouvelle approche de la réfraction subjective, dénommée « Digital Infinite RefractionTM » (1). Ainsi, pour la détermination du cylindre, une méthode vectorielle, à la fois plus cohérente et plus précise, a pu être développée. L’objet de cette publication est d’en présenter les principes et d’en expliquer la logique.
Dans ce premier article, nous rappellerons la définition vectorielle de la réfraction et sa représentation dans l’« Espace Dioptrique ». Puis, nous comparerons, de manière générale, les méthodes de la « Réfraction Traditionnelle » et de la « Digital Infinite RefractionTM ». Ensuite, dans une deuxième partie (et un deuxième article), nous décrirons en détail les techniques utilisées dans la « Réfraction Traditionnelle » et la « Digital Infinite RefractionTM » pour la recherche de l’axe du cylindre et pour la recherche de la puissance du cylindre. Enfin, dans une troisième partie (et un troisième et dernier article), nous décrirons le principe et la logique de la nouvelle méthode de détermination du cylindre proposée par la « Digital Infinite RefractionTM », en comparaison avec la méthode de la « Réfraction Traditionnelle » et discuterons de son application au développement d’un algorithme automatisé de recherche du cylindre.
C’est donc à une découverte approfondie et à une description détaillée d’une nouvelle méthode vectorielle de détermination du cylindre correcteur que nous vous convions. Précisons que pour la parfaite compréhension du contenu de cet article il est nécessaire d’avoir une bonne connaissance et compréhension des principes classiques de base de la réfraction.
(*) Réfracteur Vision-RTM 800 à variations continues de puissances d’Essilor Instruments
1) Représentation vectorielle du cylindre dans un espace dioptrique
Expression « Polaire » vs expression « Cartésienne » de la réfraction :
S’il est de tradition, en optique ophtalmique, d’exprimer la formule d’une réfraction par son « expression polaire » - sphère, cylindre et axe -, il est aussi possible d’en donner une « expression cartésienne » sous la forme de 3 coordonnées :
1) la sphère équivalente ou sphère moyenne M, égale à la puissance de la sphère augmentée de la moitié de celle du cylindre,
2) la composante du cylindre selon l’axe horizontal à 0° (J0°), représentant la composante directe / indirecte de l’astigmatisme,
3) la composante oblique du cylindre selon l’axe oblique à 45° (J45°), représentant la composante oblique de l’astigmatisme.
Cette « expression cartésienne » présente l’avantage d’exprimer la formule réfractive sous la forme de 3 composantes indépendantes les unes des autres et exprimées, toutes trois, dans une unité unique et cohérente, la dioptrie. Celles-ci peuvent avantageusement remplacer les composantes de l’expression polaire classique de la réfraction - sphère, cylindre et axe - qui sont interdépendantes et exprimées dans des unités différentes, en dioptries pour la sphère et le cylindre et en degrés pour l’axe. Par ailleurs, l’expression cartésienne donne de la réfraction une formule globale unique qui en facilite l’analyse et les comparaisons statistiques (2).
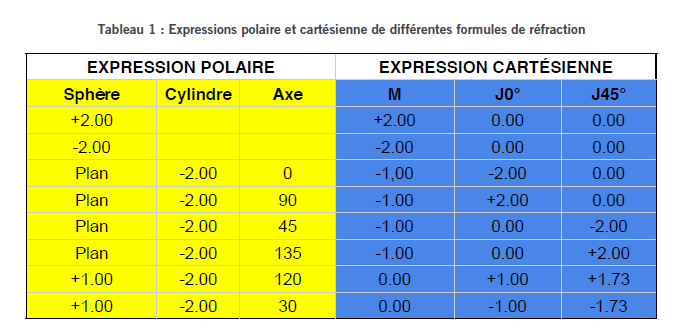
A titre d’illustration, on pourra consulter le tableau 1 qui donne quelques exemples de transposition en coordonnées cartésiennes de formules de réfraction exprimées en coordonnées polaires classiques. A la lecture de ce tableau, on pourra constater que l’expression cartésienne d’une formule réfractive consiste, en quelque sorte, à exprimer la réfraction sous la forme d’une composante moyenne et de deux composantes cylindriques pures - c’est-à-dire dont les sphères moyennes nulles et similaires à des formules de cylindres croisés de Jackson - dont l’une, à 0° / 90°, représente la composante horizontale / verticale de l’astigmatisme et l’autre, à 45° / 135°, représente la composante oblique de l’astigmatisme.
La relation qui lie les deux expressions polaire et cartésienne d’une même formule de réfraction relève d’un simple calcul de trigonométrie et il est relativement aisé de passer d’une expression à l’autre :
– Si on connait la formule polaire classique de la réfraction Sph ( Cyl ) Axe, on pourra calculer les trois coordonnées de son expression cartésienne au moyen des 3 formules suivantes :
- M = Sph + Cyl / 2 ;
- J0° = Cyl * Cos (2 * Axe) ;
- J45° = Cyl * Sin (2 * Axe).
On remarquera qu’en raison du cycle non trigonométrique de l’axe - c’est-à-dire de sa variation de 0 à 180° et non de 0° à 360° -, il est nécessaire de doubler la valeur de l’axe du cylindre.
– Inversement, si on connait les deux composantes cartésiennes du cylindre, J0° et J45°, il est aisé de retrouver ses composantes polaires, cylindre et axe, par composition vectorielle ; et pour la sphère, il suffit de soustraite algébriquement la moitié de la valeur du cylindre à celle de la sphère équivalente, pour en trouver la valeur. Les formules sont alors les suivantes, en convention de cylindre négatif :
- Sph = M – Cyl / 2
- Cyl = – √JO°² + J45°²
- Axe = 0,5 * Arc Tan (J45° ⁄ JO°) + C, avec C constante égale à 90 si J0° > 0 et égale à 0 si J0° < 0.
Pour des raisons de simplicité de compréhension et de facilité de représentation graphique, nous avons choisi, dans cette publication, de ne pas retenir de pondération de ½ entre les valeurs des composantes J0° et J45° du cylindre, d’une part, et la puissance sphérique équivalente M d’autre part, comme cela est généralement le cas dans la littérature sur l’expression vectorielle de la réfraction. Le principe reste le même mais la compréhension en est ainsi facilitée.